La serie:

Le prove dell’inesistenza di dio

Bentornati e preparatevi a un viaggio nel multiverso del possibile, da esplorare senza bisogno di strani vascelli, ma solo con l’immenso potere della Logica. Un’esplorazione che vi permetterá di guardare dritto negli occhi l’apologeta che vi chiede “ma é almeno possibile che dio esista?” e rispondere con sicurezza un secco no.

Logi-che?

Parliamoci chiaro: il cervello umano non é una perfetta macchina razionale. Non si é evoluto per fare calcoli istintivamente accurati e chiunque creda il contrario puó provare a calcolare a occhio le prime 45 cifre di pi greco. Cosí, a istinto, senza far conti o simili.

…

Eh, giá. Difficile, vero? Serve una formula per farlo.

Perché abbiamo dette formule? Perché sappiamo che quando si tratta di numeri il nostro cervello é inaffidabile. Ecco, lo stesso vale per i ragionamenti. E anche per i ragionamenti ci sono algoritmi e formule dedicati che si possono usare. Sono cosí robusti e sicuri che abbiamo “insegnato” a farli anche ad ammassi di minerali, metalli e plastiche che chiamiamo “chip”.

É stata infatti proprio una rivoluzione nella logica che ha permesso la nascita del computer!

Quindi é il momento di esplorare questa logica, lo faremo iniziando dai simboli che si usano.

Le proposizioni

Alla partenza ovviamente abbiamo le proposizioni, le affermazioni, cose come “M(x,y)”, ovvero una frase che dice qualcosa di x e y. Per esempio diciamo che C(lettore,concetto), significa che “il lettore ha capito il concetto” ed é vera se e soltanto se chi legge sta capendo il concetto.
Ora, se volete avere un momento tipo “la storia infinita” dove andate a gridare alla finestra di aver capito, io non lo impediró, giuro.
Ma chi lo decide se chi legge sta veramente capendo? Alla logica questo non interessa. Quello che interessa é che la proposizione puo’ essere “vera” o “falsa” e come le varie operazioni mettono insieme proposizioni “vere” e “false” per produrne di piú complesse a loro volta “vere” o “false”.

Le operazioni

Incamminandoci in avanti troviamo altri simboli, alcuni sembrano simboli alieni, poco familiari, altri sono normali segni di punteggiatura.

◇ □ ∃ ∀ ⊥ → ¬ ∧ ∨ ()

É importante non farsi spaventare da questi simboli, questa roba é facilissima, la potrebbe capire pure un bambino. Niente di quello che discuteremo arriva ad essere tanto complicato quanto un’elevazione a potenza o una radice quadrata, quindi se avete superato la seconda media potete capire questi concetti. E chi non l’ha fatto pure ci puó riuscire, con un minimo di impegno. Per chi invece questa roba giá la conosce, saltate avanti.

Per indicare le cose a cui questi segni si applicano senza complicarci troppo la vita, le indicheró con dei puntini. Quindi per fare un paragone con l’aritmetica (…) significa che le parentesi si applicano a qualcosa al loro interno e …+… significa che + si mette in mezzo a due cose a cui viene applicato.

Dalle basi…

Ok, iniziamo dalla parte facile-facile-facile: le parentesi (…) e la t sottosopra ⊥.
Le parentesi… sono parentesi, funzionano come parentesi in matematica, fine. Le operazioni dentro si risolvono prima di quelle fuori. Che operazioni? tutti gli altri simboli essenzialmente.
La ⊥ invece é uguale a “falso”. Senza se e senza ma, é solo un altro modo di scrivere “falso”. Quando fai uscire la ⊥ é game over, sei arrivato a una contraddizione e almeno un’ipotesi deve essere falsa.

Ok, ora la parte facile-e-basta: le congiunzioni …∧… e …∨… e la negazione ¬… . La negazione é semplicissima, corrisponde al “non”. “¬ vero” uguale “falso” e “¬ falso” uguale “vero”. Le congiunzioni sono equivalenti alla nostra “e” ed “o”, rispettivamente ∧ ed ∨. Con un distinguo: la “o” la usiamo sia per situazioni mutuamente esclusive sia per situazioni inclusive, ecco, la “o” della logica é sempre inclusiva. Quindi “vero ∨ vero” uguale “vero”.
Tra poco metto una tabellina per ricordare le cose piu’ facilmente… ma dopo il prossimo paragrafo, giurin giurello.

Adesso iniziamo a complicarci un minimo la vita e arriviamo alla roba con una difficoltá media: l’implicazione …→… .
Questo e’ equivalente al “se… allora…”. E esattamente come per il “se… allora…” non esprime la veritá di nient’altro che di una relazione tra le proposizioni coinvolte. Non importa se il “se” sia vero o falso, non importa se l’ “allora” sia vero o falso, importa se il “se” rende vero l’ “allora” ogni volta che succede. Questo significa che l’unico caso in cui possiamo avere che qualcosa con → é uguale falso é il caso “vero→falso”. Notare che questo non e’ un “se e solo se… allora…”, quindi possiamo anche avere che “falso→vero” sia uguale a “vero”.

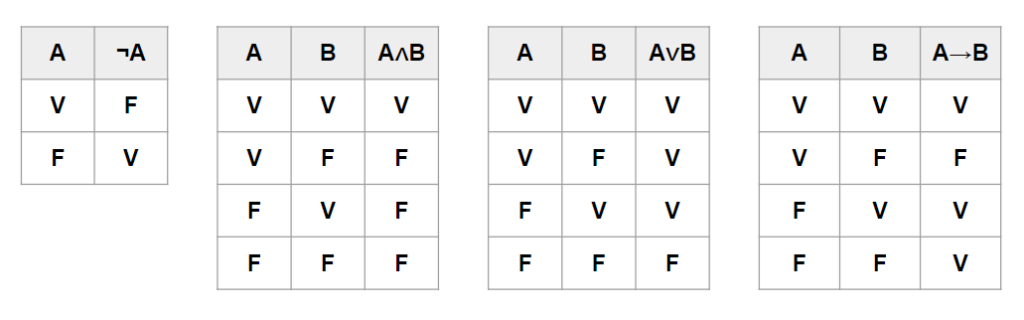
Ecco, se siete arrivati a questo punto, congratulazioni: avete scalato la cima della Logica Proposizionale. Da questa vetta potete ammirare il 90% delle proposizioni che vi troverete davanti nella vita e distinguere facilmente quelle valide da quelle non valide. Fallacie come l’affermazione del conseguente o la negazione dell’antecedente sono chiaramente distinguibili semplicemente tenendo a mente la definizione di →. Ci sono peró ancora delle terre oscure su questo pianeta, che val la pena esplorare, quelle delle fallacie basate sulle quantitá, sui “tutti”, sui “nessuno” etc.

Alle vette

E qui arriviamo a roba che in matematica si fa studiare a un quattordicenne: i quantificatori, ovvero quelle buffe letterine al contrario ∃…(…) ed ∀…(…) . Partiamo da ∀…(…) questa significa “tutti gli … sono …”. Complicato? No, se era tutto qui questa la discutevamo prima.
La complicazione arriva quando ci volete mettere vicino un ¬ e fare qualcosa tipo ¬∀…(…). In quel caso diventa “non tutti gli … sono …”.
Qui a tantissimi esplode il cervello o qualcosa del genere, perché sbagliano di continuo e dicono che questo significa “nessun … é …”. Invece la risposta giusta e’ “almeno un … non é ….” ovvero ∃…(¬…).
E si perche’ ∃…(…) significa “almeno un … é …”. Anche qui similmente a prima possiamo mettere un “non” e trovarci ¬∃…(…) che significa “non almeno un … é …” e quindi “tutti i … non sono …”.
∀ é anche noto come “per ogni” e ∃ viene detto pure “esiste”.

Bene, con questo decollo siamo entrati nell’orbita del pianeta Logica del Primo Ordine, se imparate anche questi e li tenete sempre a mente potrete riconoscere anche dallo spazio quando qualcuno commette fallacie come quella che “se ogni cosa nell’universo ha una causa, allora ci deve essere una causa di tutte le cose”.

Verso l’infinito e oltre

E parlando di orbita, é tempo di partire finalmente per il multiverso del possibile. Ecco gli operatori modali ◇… ed □… . Qui siamo effettivamente a qualcosa di complicato non tanto per la complessitá delle operazioni coinvolte, quanto piuttosto per la difficoltá a tradurre questi operatori in parole, visto che sono usati in tante situazioni diverse. Quindi per semplificarci la vita, vi parleró solo della nostra situazione, quella rilevante a questa discussione. In altre parole del loro uso per rappresentare possibilitá e necessitá.

Specificamente abbiamo che ◇… significa “possibilmente …”, ovvero che da qualche parte nel multiverso c’é un mondo in cui … é vero. Doctor who scansate, spiderverse non ti accostare neanche, il nostro multiverso non ha solo illimitate possibilitá, le ha tutte.
Dalla prima all’ultima, senza eccezioni, da qualche parte nel nostro multiverso se é possibile c’é un mondo in cui é vero. Questo significa che da qualche parte c’é un mondo possibile in cui ruby é davvero imparentata a mubarak, ma nessun mondo in cui i triangoli hanno quattro lati. Quindi “◇ ruby” uguale “vero” ma “◇ quadritriangoli” uguale falso. O piú formalmente “◇ ⊥” uguale falso e tutto il resto é vero.

E adesso parliamo di necessitá: □… significa infatti “necessariamente …”. Cosa vuol dire? vuol dire che se qualcosa é necessariamente vero, non importa dove andiamo nel multiverso del possibile, ce lo ritroviamo, peggio di silvio in tv durante quell’offesa al pudore che sono stati i suoi funerali di stato. Peggio delle campane alla domenica mattina. Peggio della co2 industriale nell’atmosfera. Letteralmente in ogni mondo possibile, vale a dire che la negazione di una cosa necessaria é essa stessa impossibile, che é una contraddizone. In altre parole se é vero “□ triangolitrilateri” allora é sempre falso “¬triangolitrilateri” insomma piú formalmente “□¬⊥” uguale vero e il resto é falso.

Questo completa la nostra esplorazione del multiverso del possibile e adesso che abbiamo una mappa dell’intera Logica Modale possiamo vedere se dentro un dio ci sta oppure no. E possiamo farlo con un’altra delle mie 49 dimostrazioni.

404, Dio non trovato.

NOTA: dato che l’unica regola utilizzata dalla logica modale é l’equivalenza ◇¬p a ¬□p, e’ valida in TUTTE le logiche modali.

Chevvordí?!? ecco, avete presente quando vi dicevo che □ e ◇ si usano in tante situazioni? Questo sta dicendo che quanto segue vale in tutte.

Premesse:

p1: ◇∃x(∀y( ¬M(y,x) ) ) : possibile esistenza di un ente per cui una azione M non e’ possibile da parte di alcun soggetto (eg: masso inamovibile, arbitrio incoercibile)

In altre parole, stiamo dicendo che nel nostro multiverso del possibile c’é da qualche parte almeno un qualcosa tale che tutti i soggetti non sono capaci di fargli una certa cosa M. Come esempi possiamo avere il solito scudo impenetrabile, ovvero uno scudo che niente e nessuno puó penetrare, uno scudo la cui natura impedisce a tutti e tutto di penetrarlo. Nota: non stiamo dicendo che esiste nel mondo reale.

p2: □( ∀x(O(x)→∀y( M(x,y) ) ) ) : applicazione della definizione di onnipotenza rispetto alla capacita’ di effettuare una certa azione M su ogni soggetto (eg: muovere ogni cosa, coercire ogni arbitrio), essendo una definizione é valida necessariamente

Qui insomma si dice che necessariamente in tutti gli enti se l’ente in questione é onnipotente, allora su tutte le cose quell’onnipotente é capace di fare una certa cosa M. In altre parole stiamo dicendo che é vero che l’essere onnipotenti da (tra le varie) la capacitá di fare una certa cosa su tutto e tutti in ogni mondo possibile. Un esempio di queste capacitá universali puó essere ad esempio la capacitá di penetrare con una lancia ogni cosa. State giá intuendo dove andiamo a parare, vero? Ma, in logica l’intuito non vale niente, bisogna vedere che ne dice il calcolo.

p3: O(D) : asserzione che dio e’ onnipotente

Ultima premessa: dio é onnipotente. Questa é una semplice proposizione e stiamo assegnandogli come valore “vero” per vedere cosa comporta assieme alle altre premesse. In altre parole di tutto quello che abbiamo presentato fin ora ci stiamo chiedendo “cosa implica la veritá di queste proposizioni?”. Calculemus (cit. Leibnitz).

Lemmi:

l1.1: ◇∀y( ¬M(y,R) ) : Instanziazione di R per regola di Quantificazione Esistenziale (Skolemizzazione) in p1

Qui cominciamo a svolgere le operazioni. Abbiamo detto in p1 che nel nostro multiverso del possibile c’é da qualche parte almeno un qualcosa tale che tutti i soggetti non sono capaci di fargli una certa cosa M. Ecco, ora gli diamo un nome. Quel nome é R. Invece di chiamarlo “quella cosa che abbiamo detto che esiste che fa cosí e cosá”, lo chiamiamo R.
R insomma é il nome del nostro scudo impenetrabile. Lo so, ci sono nomi piú belli da dare a artefatti possibili, ma in logica si usano le singole lettere.

l1.2: ◇ ¬M(D,R) : Istanziazione di D per regola di Quantificazione Universale in l1.1

Qui invece facciamo una cosa diversa. in l1.1 abbiamo detto che a questo R tutti i soggetti non sono capaci di fargli una certa cosa. Ecco, tutti deve includere D, altrimenti sarebbe alcuni e non tutti. Quindi siamo arrivati a dire che nel nostro multiverso del possibile c’é un mondo in cui dio D non ha la capacitá di fare una certa cosa M a un oggetto R. Che nel nostro esempio significa che se lo scudo impenetrabile esiste, nemmeno dio puó penetrarlo. Il che, se ben ci pensate, non é altro che una naturale conseguenza della definizione di impenetrabile. Ma adesso l’abbiamo calcolato.

l1.3: ¬□ M(D,R) : equivalenza di ◇¬p a ¬□p

Vi ricordate quando abbiamo detto che ∃…(¬…) era uguale a ¬∀…(…)? Per possibilitá e necessitá funziona uguale. Insomma ◇¬… é uguale a ¬□… e qui stiamo semplicemente applicandolo per trasformare l1.2 in quanto segue: non é necessario che D abbia la capacitá di fare una certa cosa M a R. Notate una cosa peró: prima stavamo parlando di un mondo nel multiverso del possibile, ora stiamo parlando di ogni universo, stiamo parlando di cosa é necessario e cosa no. Quindi stiamo parlando anche di questo mondo qui, dove siamo io e te in carne e ossa. In questo mondo diciamo che non é il caso che necessariamente dio possa fare qualcosa. Cioé nel nostro mondo non é necessario, ad esempio, che dio possa trafiggere uno scudo impenetrabile.

l2.1: □(O(D)→∀y( M(D,y) ) ): Istanziazione di D per regola di Quantificazione Universale in p2

Ora torniamo indietro e andiamo a guardarci p2, quella riguardava tutti gli enti onnipotenti, ma noi vogliamo adesso parlare di uno in particolare: dio. Quindi sostituiamo alla x la nostra D. E ci troviamo a dire che necessariamente se dio é onnipotente, allora per tutti gli oggetti ha la capacitá di fargli una certa cosa M.
Nel nostro esempio quindi questo si tradurrebbe nel fatto che tra le conseguenze dell’onnipotenza di dio é inclusa quella di poter sempre e comunque penetrare qualsiasi cosa o persona (si, senza neanche consenso, chiedete a maria porella).

l2.2: □( O(D)→M(D,R) ): Istanziazione di R per regola di Quantificazione Universale in p2

Ma anche qui c’é un tutti che quindi deve includere il nostro R di cui abbiamo giá parlato in precedenza. Quindi applichiamo l2.1 proprio al suo caso specifico e ci ritroviamo a dire che necessariamente se dio é onnipotente, allora ha la capacitá di fare una certa cosa M anche a R.
Ovvero l’onnipotenza divina non ammette eccezioni e quindi non puo’ ammettere nemmeno l’eccezione di R, quindi dio se é onnipotente allora deve poter penetrare anche il nostro scudo dal multiverso del possibile.

l3.1: □( M(D,R) ) : modus ponens da p3 e l2.2

Ecco che ci avviamo alla chiusura. Ora é il momento di applicare una delle regole fondamentali della logica, che puó essere dimostrata con le tabelline di sopra se uno ci si mette, il modus ponens. L’essere onnipotente di dio e il fatto che necessariamente il suo essere onnipotente implica che abbia la capacitá di fare la certa cosa M su R, messi assieme risultano inevitabilmente nell’affermazione perentoria che necessariamente dio puo’ fare la certa cosa M su R.
Quindi siamo arrivati a calcolare che dio puó penetrare anche il nostro bello scudo possibile.

La conclusione

l3.2: ⊥ : contraddizione tra l3.1 e l1.3

Ed eccoci qua. L’abbiamo ritrovato mr game over, il simbolo ⊥. Ricordate cosa abbiamo detto? se compare, una delle ipotesi deve essere sbagliata, ma come mai é comparso? É comparso perché abbiamo dedotto dalle premesse sia un’affermazione (l3.1) che la sua negazione (l1.3). In altre parole abbiamo calcolato sia che non é necessario che D abbia la capacitá di fare una certa cosa M a R, sia che é necessario che D abbia la capacitá di fare la certa cosa M su R.
Nel nostro esempio questo equivale a dire che deve sia essere possibile che esista uno scudo impenetrabile anche a dio, sia essere impossibile. E una certa cosa non puo’ essere possibile e impossibile allo stesso tempo, quindi abbiamo una contraddizione, un assurdo, un paradosso.

Eccoci quindi alle conclusioni: almeno una delle premesse deve essere falsa.
Le opzioni sono 3. O p1, o p2 o p3.

Partiamo con p1: quella affermava che nel multiverso del possibile c’é almeno un ente per il quale sia tutti gli altri enti non hanno la capacitá di fare una certa cosa M. Se é falsa, allora deve essere anche concettualmente impossibile che esistano una roccia inamovibile, un arbitrio incoercibile o uno scudo impenetrabile. Eppure questi concetti ci sono ben chiari e lo stesso enunciare tali concetti e constatare che corrispondono alla descrizione data in p1 basta ad assicurarci che p1 non sia falsa.

Forse p2 allora? Dovremmo quindi concludere che l’onnipotenza non garantisce necessariamente a dio la capacitá di compiere una azione su qualsiasi oggetto, ovvero l’onnipotenza non comporta la capacitá di muovere ogni cosa o di coercere ogni arbitrio o penetrare tutto e tutti in ogni mondo possibile? C’é un problema anche qui. La definizione di onnipotenza comporta oggettivamente queste capacitá. (di nuovo, chiedete a maria)

Ed eccoci dunque alla fine: rimane solo una possibilitá, negare p3 e quindi dire che non c’é nessun D tale che O(D), in altre parole dobbiamo concludere che un dio onnipotente non esiste.
Come Volevasi Dimostrare.